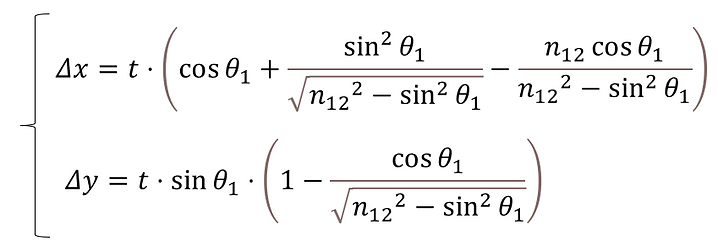Relationships derived from Snell's law
-
Image position of a light ray incident on a material
The light rays before and after entering the material are shown in the figure below.
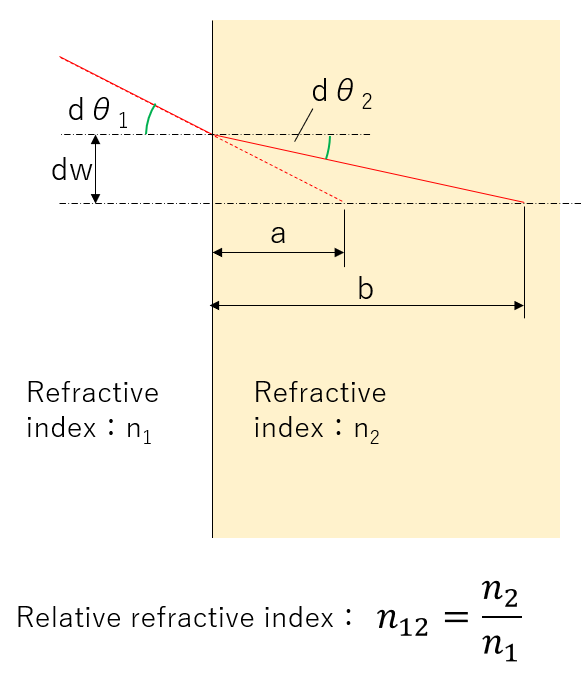
Here, dw, dθ1 , and dθ2 are small quantities.
The conditions shown in the figure can be expressed as follows:
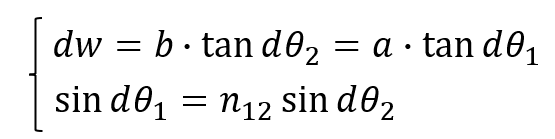
Here,

Therefore,
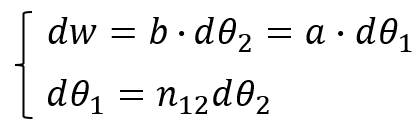
Therefore,

-
Image position when a parallel plate is placed perpendicular to the optical axis
Consider the following light beam that enters a plane-parallel plate and forms an image at the exit point. Calculate s in this case.
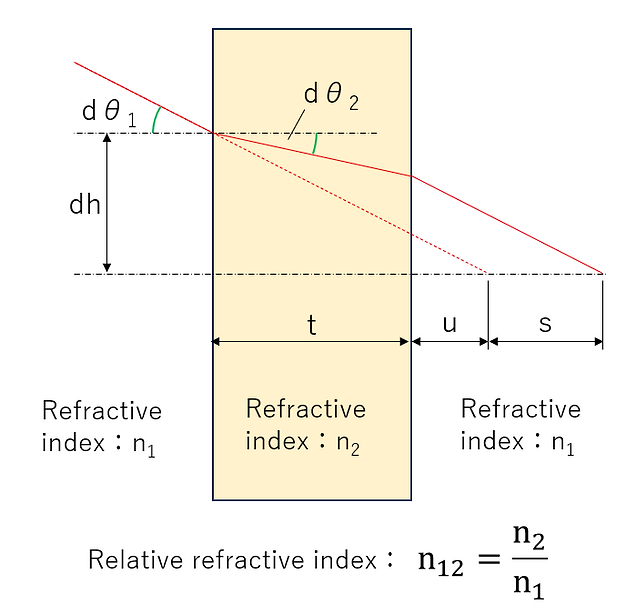
Here, dh, dθ 1 , and dθ 2 are small quantities.
The conditions shown in the figure can be expressed as follows:
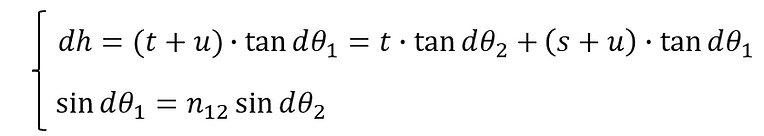
Where:
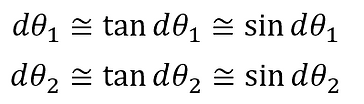
Therefore,
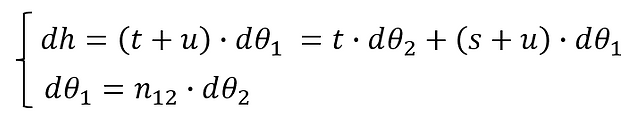
Therefore,
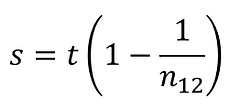
-
Image position when a parallel plate is placed at an angle to the optical axis
Consider the following light beam that is obliquely incident on a parallel plane plate and forms an image at the exit point. Calculate Δx and Δy in this case.
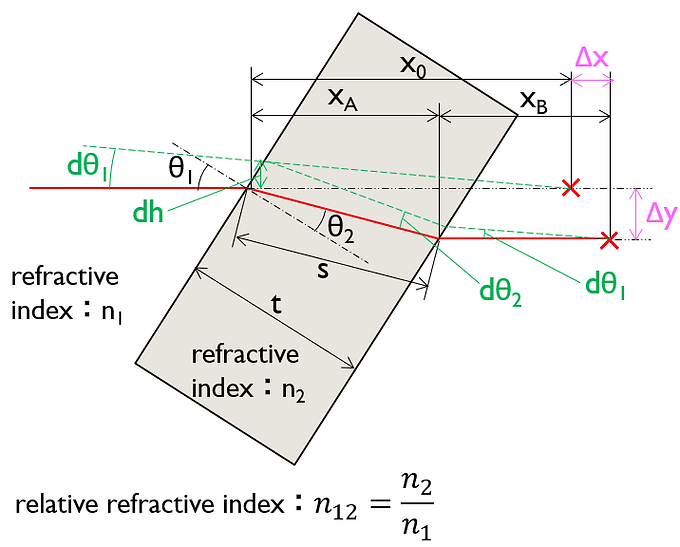
Here, dh, dθ 1 , and dθ 2 are small quantities.
The conditions shown in the figure can be expressed as follows:
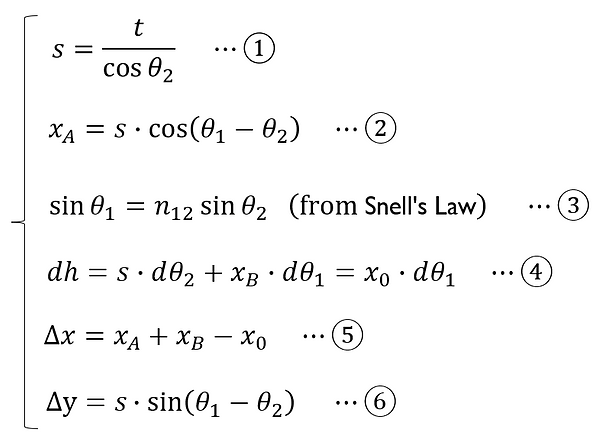
Differentiate both sides of ③ to get
From ①, ②, ③', ④, and ⑤, eliminating s, xA, xB, dh, dθ1, and dθ2, we get
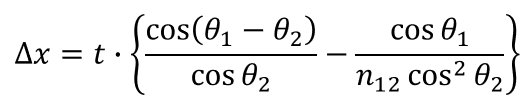
Here, from ① and ⑥,
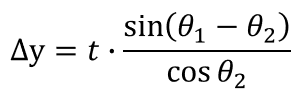
Also, from ③,
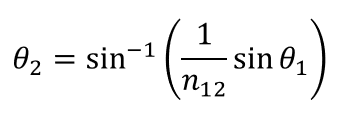
Therefore, the solution we seek can be expressed as follows:

Furthermore, by applying ③ and eliminating θ2, we get